Binary Search Trees

Let us implement in julia 0.6.0 a binary search tree to store integers. Each node is either of type Nil or of type bst, as declared below. Type Nil is used a null pointer. We use type union MayBe to hold either a Nil() or a bst. At the start the tree is empty so it is initialized to Nil(). Removing the type declaration from the data element should be sufficient to store datatypes for which a comparator is implemented.

type Nil end
MayBe{T} = Union{T,Nil}

type  bst 
    data::Int
    left::MayBe{bst}
    right::MayBe{bst}
end

global root = Nil()                # root of the BST

Find

Order property states that at every node, the left sub tree contains smaller values, and the right subtree contains larger values. So, it is straightforward to branch, given a key and the value stored at a node. Below is a recursive implementation of find

function find(node::MayBe{bst}, key::Int)
    if (typeof(node) == Nil)
        return false
    end
    
    if (node.data == key)
            return true
    end
    
    if (key < node.data)
        find(node.left, key)
    else
        find(node.right, key)
    end
end

Insert

We assume that duplicates are not allowed. To insert a node we branch as in the case of find. Once we have located the pointer (identified by type Nil), we attach a new single node bst object. If the insertion occurs in the left subtree then the left pointer of the node is updated. The right pointer is updated if the insertion occurs in the right subtree. We return the modified tree in each recursive step. This has to do with how arguments are passed by value in julia.

function ins(node::MayBe{bst}, d::Int)    # insert d in the BST rooted at node

   if (typeof(node)==Nil) 
        node = bst(d, Nil(), Nil())          # attach a new BST with data d
        return node
   end
   
   if (d == node.data)
        return node            # d already in the tree, no insertion 
   end
    
   if (d < node.data )      # check whether insert is in left/right subtree
        node.left = ins(node.left, d)
   else
        node.right = ins(node.right, d)
   end 
   return node         # reference needed to reassign the node
    
end

The sequence of insertions below (in array A) should give a balanced binary search tree.

global root = Nil()
A = [4,2,6,1,3,5,7]
for i=1:length(A)
    root = ins(root,A[i])      # note the assignment to root, BST updated
    println(root)
end

bst(4, Nil(), Nil())
bst(4, bst(2, Nil(), Nil()), Nil())
bst(4, bst(2, Nil(), Nil()), bst(6, Nil(), Nil()))
bst(4, bst(2, bst(1, Nil(), Nil()), Nil()), bst(6, Nil(), Nil()))
bst(4, bst(2, bst(1, Nil(), Nil()), bst(3, Nil(), Nil())), bst(6, Nil(), Nil()))
bst(4, bst(2, bst(1, Nil(), Nil()), bst(3, Nil(), Nil())), bst(6, bst(5, Nil(), Nil()), Nil()))
bst(4, bst(2, bst(1, Nil(), Nil()), bst(3, Nil(), Nil())), bst(6, bst(5, Nil(), Nil()), bst(7, Nil(), Nil())))

Delete

Helper function min find the minimum value in the right subtree at any given node. We use this minimum value in the delete function.

function min(node::MayBe{bst})  # returns Int, never called on empty BST
    while (typeof(node.left) != Nil)
        node = node.left
    end
    return node.data               # left most element
end

To delete an element we proceed as in find. If the element is not found, and we end up with a Nil type then return the original tree. Otherwise, three cases are to be considered.

• The node to be deleted is a leaf node: in this case, we return the Nil(), which is assigned to the appropriate subtree of the parent, thereby deleting the node.

• The node to be deleted has a single child: in this case return either the left or the right subtree.

• The node has two children. We find the minimum element in the right subtree, and delete it from the right subtree. The resulting subtree is now the right child of the node, and the value at the node can be replaced by the minimum value in the right subtree.

function del(node::MayBe{bst}, d::Int)
   if (typeof(node)==Nil)
        return node
   end
   
     if ((d == node.data) && (typeof(node.left) == Nil) && (typeof(node.right) == Nil))
        return Nil()                   # node to be deleted is a leaf
    end
    
    if ((d == node.data) && (typeof(node.left) == Nil))   # node to be deleted has one child
        return node.right
    end
    
     if ((d == node.data) && (typeof(node.right) == Nil)) # node to be deleted has one child
        return node.left
    end
    
    
    # node to be deleted has two children
    if ((d == node.data) && (typeof(node.left) != Nil) && (typeof(node.right) != Nil))
          m = min(node.right)            # find the min in the right subtree                    
          node = del(node, m)            # delete it recursively
          node.data = m                  # copy the min to the current node 
          return node
    end
    
    
   if (d < node.data)
        node.left = del(node.left, d)
    else
        node.right = del(node.right, d)
    end
    return node
end

The sequence of deletions below should give an empty tree.

A = [4,2,6,1,3,5,7]
for i=1:length(A)
    root = del(root, A[i])
    println(root)
end

bst(5, bst(2, bst(1, Nil(), Nil()), bst(3, Nil(), Nil())), bst(6, Nil(), bst(7, Nil(), Nil())))
bst(5, bst(3, bst(1, Nil(), Nil()), Nil()), bst(6, Nil(), bst(7, Nil(), Nil())))
bst(5, bst(3, bst(1, Nil(), Nil()), Nil()), bst(7, Nil(), Nil()))
bst(5, bst(3, Nil(), Nil()), bst(7, Nil(), Nil()))
bst(5, Nil(), bst(7, Nil(), Nil()))
bst(7, Nil(), Nil())
Nil()

Average times

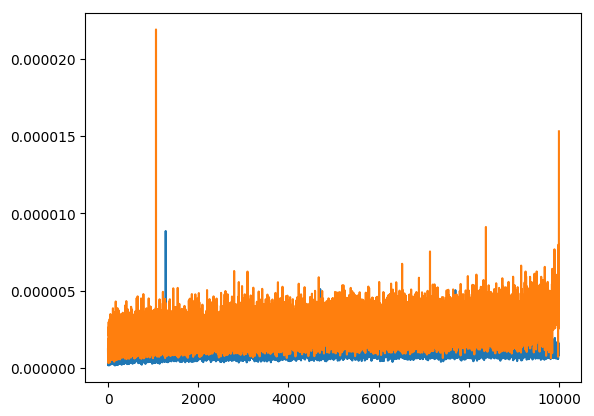
We can also plot the time it takes for random insertions and then random deletions. The insertions are in blue and the deletions are in yellow.

using PyPlot

size = 10000
y=zeros(size)

inp = randperm(size)

root =Nil()
ctr = 1
for j in inp 
    y[ctr] = @elapsed    root = ins(root,j)
    ctr = ctr + 1
end


p = plot( y)

ctr = size
for j in inp[1:size-1] 
    y[ctr] = @elapsed    root = del(root,j)
    ctr = ctr - 1
end

p= plot( y)


#for i=1:size
#     y[i] = @elapsed    root = ins(root,i)
#end

#p = plot(y)

The code is available here.