“All your proof are belong to us“
The first way we learn to do proofs is by induction. Proofs by induction are done in three steps. First, we establish a base case. Next we assume a hypothesis, and finally, we prove the inductive step. As an example let us consider the fact that the sum $0+1+2+ \ldots+n$ is $n(n+1)/2$. The three steps are:
Base case: consider the series $0+1$, the sum is $1$, and the formula is $1(2)/2$. So, the formula and the actual series sum agree.
Induction hypothesis: let’s assume that $0+1+\ldots + (k-1)$ is $k(k-1)/2.$
Inductive step: we want to show that the sum $0+1+2+ \ldots + k$ is $k(k+1)/2$. By our hypothesis the series sum is $k(k-1)/2 + k = k(k+1)/2$.
The proof above is clear enough for us. The question is whether the proof above is machine readable and verifiable. In the ordinary course, we write programs and argue for the correctness of these programs. What if, we were able to write a program which could be verified by another program? Interestingly enough programs can be written to provide proofs, as is illustrated next.
Here is a short program in a functional programming language
coq to compute the sum of the first $n$ integers.
Require Import Arith.
Fixpoint sum (n:nat) : nat :=
match n with
| 0 => 0
| S m => n + sum m
end.
Compute (sum 10).
nat is a type which represents natural numbers. The
natural numbers are 0, S 0, S S 0, ... where S is the
type constructor. The code is recursive, and the base case along with
the recursive step is specified using the construct match
(for template matching). The last line Compute (sum 10) computes
the sum $0+1+\ldots +10$.
Typically, we would prove that the program above is correct by writing an induction proof as the one listed above. We can also specify the proof in specification language such as ‘Gallina.’ A Gentzen style proof system can be used to verify each step. We specify the proof as a sequence of steps. Every step follows from the previous step given the rules in the proof system. Machine verification of inductive proofs is interesting. Not only we can check for bugs, they can also be graded automatically.
The method is illustrated next. Think of Gallina as specifying a proof, rather than discovering a proof using an automated process. If
the coq compiler accepts the specification, then the
proof is valid otherwise it is not. The proof discovery process
cannot usually be automated because of undecidability
issues.
Let us start with a few basic facts about the type nat. We will
use these Lemmas later in the final specification.
Let us first prove
that sum (S n) = (S n) + (sum n). The specification of the proof
of this fact in Gallina is below.
Lemma l1: forall n:nat, sum (S n) = (S n) + (sum n).
Proof.
induction n as [|m IH].
- (*2*0 = 0 *) simpl. reflexivity.
- (* 2*sum(n) = 2n + sum(n-1) *) rewrite -> IH. simpl. reflexivity.
Qed.
The lemma itself is a statement in predicate
logic. The proof starts with Proof and ends with Qed. This is an
inductive proof on n, as specified by the keyword induction. The
as clauses identifies the two subgoals that need to be proven. The
goals are within [] and separated by |. In the first empty goal
to the left of |, n is replaced with 0. In the second subgoal called
IH, nis replaced withS m.` The two subgoals are proved
in the two bullets. Simplification and the reflexivity establish the base case. Now, let us examine the second subgoal. The goal is below the
horizontal line, and the assumptions are above the horizontal line.
1 subgoals
m : nat
IH : sum (S m) = S m + sum m
______________________________________(1/1)
sum (S (S m)) = S (S m) + sum (S m)
Rewriting the subgoal using the induction hypothesis gives us.
sum (S (S m)) = S (S m) + (S m + sum m)
Simplification gives us
S (S (m + S (m + sum m))) = S (S (m + S (m + sum m)))
The similarity of the two terms can be verified by reflexivity.
Furthermore, let us prove that S (S n) = S (n+1).
Lemma l2: forall n:nat, S (S n) = S (n+1).
Proof.
induction n; intros. simpl.
reflexivity.
- simpl.
- rewrite <- IHn. reflexivity.
Qed.
Once again the proof is by induction on n. intros adds the variables that are quantified by the for all quantifier to the context. Use of intros is redundant here. simpl states that each subgoal should be simplified at the start. The two bullets are the two subcases.
2 subgoal
______________________________________(1/2)
2 = 2
______________________________________(2/2)
S (S (S n)) = S (S n + 1)
The first subgoal is readily proved using reflexivity. The system assumes the IH to prove the second subgoal. The rewriting of the subgoal as the commands are processed is shown below, until the LHS and the RHS are the same.
1 subgoals
n : nat
IHn : S (S n) = S (n + 1)
______________________________________(1/1)
S (S (S n)) = S (S n + 1) simplify.
S (S (S n)) = S (S (n + 1)) rewrite <- IH.
S (S (S n)) = S (S (S n)) reflexivity.
We also need the following Lemma.
Lemma l3: forall n:nat, n+1 = S n.
Proof.
induction n; intros. simpl.
reflexivity.
simpl.
rewrite <- IHn.
reflexivity.
Qed.
Finally, the proof
Theorem gauss_sum: forall n:nat, 2*(sum n) = n * (S n).
Proof.
induction n as [|m IH]; intros. simpl.
- (*2*0 = 0 *) simpl. reflexivity.
- (* 2*sum(n) = 2n + sum(n-1) *)
rewrite -> l1.
rewrite mult_plus_distr_l.
rewrite -> IH.
replace (S m) with (m+1).
replace (S (m+1)) with (2+m).
rewrite <- mult_plus_distr_r.
rewrite mult_comm.
reflexivity.
intros.
simpl.
rewrite l2.
reflexivity.
rewrite l3.
reflexivity.
Qed.
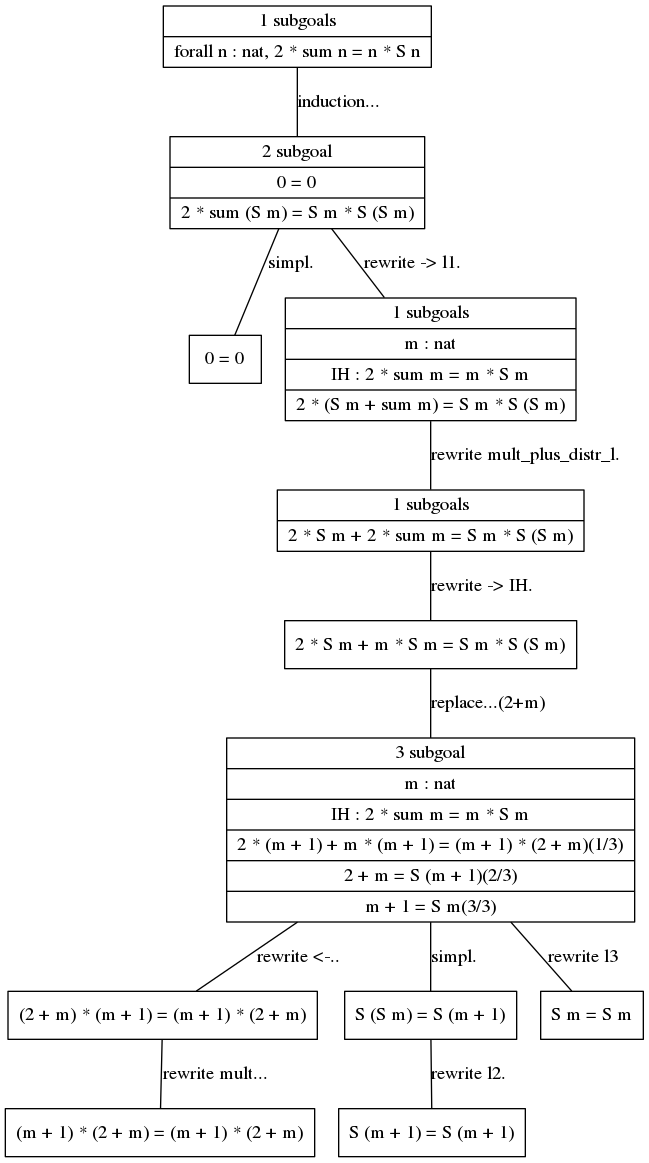
The first subgoal (the base case) can be proved easily using induction. For the second subgoal (the induction step), we have to massage the terms a lot to get them in the right shape, before reflexivity can be used. The output below shows the terms in the first column, the operation listed is in the second column.
| Subgoals | operation |
|---|---|
| 2 * sum (S m) = S m * S (S m) | rewrite -> l1. |
| r2 * (S m + sum m) = S m * S (S m) | rewrite mult_plus_distr_l. |
| 2 * S m + 2 * sum m = S m * S (S m) | rewrite -> IH. |
| 2 * S m + m * S m = S m * S (S m) | replace (S m) with (m+1). |
The replace operations creates two new subgoals: in additional to
the original term, we have to also prove that (S m) = (m+1) and
(S (m+1)) = (2+m).
3 subgoal
m : nat
IH : 2 * sum m = m * S m
______________________________________(1/3)
2 * (m + 1) + m * (m + 1) = (m + 1) * (2 + m)
______________________________________(2/3)
2 + m = S (m + 1)
______________________________________(3/3)
m + 1 = S m
The original subgoal is proved as
(2 + m) * (m + 1) = (m + 1) * (2 + m)
(m + 1) * (2 + m) = (m + 1) * (2 + m)
The next two subgoals are proved by applications of Lemma l2 and l3 respectively.
S (S m) = S (m + 1)
S (m + 1) = S (m + 1)
and as
m + 1 = S m
S m = S m
The proof tree is shown below, and the coq code is available here.
The nodes in the proof tree list the subgoals and the assumptions used to prove the subgoals. The labels on the edges correspond to the operations in the code.
Further reading: See Proofs are Programs by Walder and learn more about Curry-Howard isomorphism.