|
|
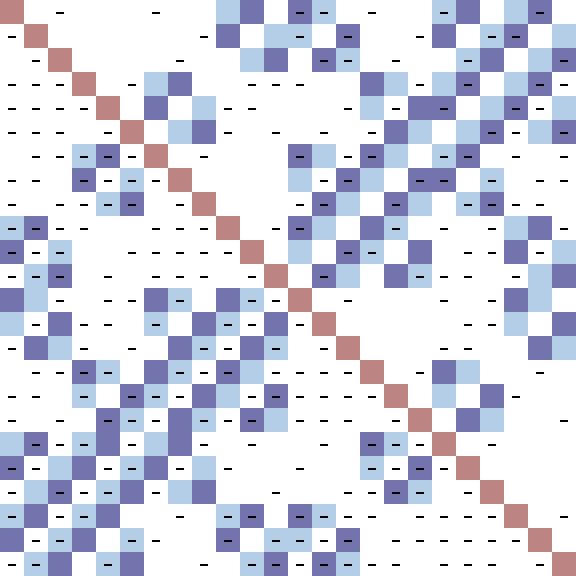
This image is of the first known OD(24;1,4,4,15). This orthogonal design was discovered by Hadi Kharaghani and W. H. Holzmann. These and many other new types of designs, but not this pretty picture, are in the paper, On the Orthogonal Designs of order 24, Discrete Applied Mathematics, 102 (2000), pp. 103-114.
The OD(24;1,4,4,15) is an orthogonal design of order 24. This means it is a 24 by 24 array, where each entry is plus or minus a variable. In the image minuses are indicated with black bars in the center of sub-squares. Orthogonal means that every distinct pair of rows sum to zero when corresponding entries are multiplied together. The 1, 4, 4, 15 numbers in the OD refer to the fact that in each row, the first variable appears once (colored brown in the image), the second variable appears four times (colored light blue), the third variable appears four times (coloured dark blue) and the fourth variable appears 15 times (coloured white).
Orthogonal designs are used in applications ranging from statistics to communications and coding theory.
Last update: 2015 April 7