A 3-d representation of K100- the complete graph on 100 vertices. Each mouse click displays a different Z-plane with edges shown in blue. The planes are organized into groups - boxes that are dx, dy apart are joined in batches defined by the variable offset. If boxes are labelled using a matrix notation with indices starting at 0, and if dx represents the "column difference" and dy the "row difference", then the Z-planes shown have the following property for a given offset value:
For dx,dy >=0, all boxes bi,j such that (i+j) = offset mod (|dx| + |dy|) are joined to their neighbour boxes at bi+dx,j+dy.
For dx<0, the pattern is slightly different: boxes bij of the form (i-j) = offset+1 mod (|dx| + |dy|) are joined to their neighbour at bi+dx,j+dy.
See the paper: Orthogonal 3-D Graph Drawing by T. Biedl, T. Shermer, S. Whitesides and S. Wismath, for details.
A 3-D VRML version of the construction is available for K16: ORTHO.WRL . A smaller construction (K9) is here: ORTHO3.WRL .
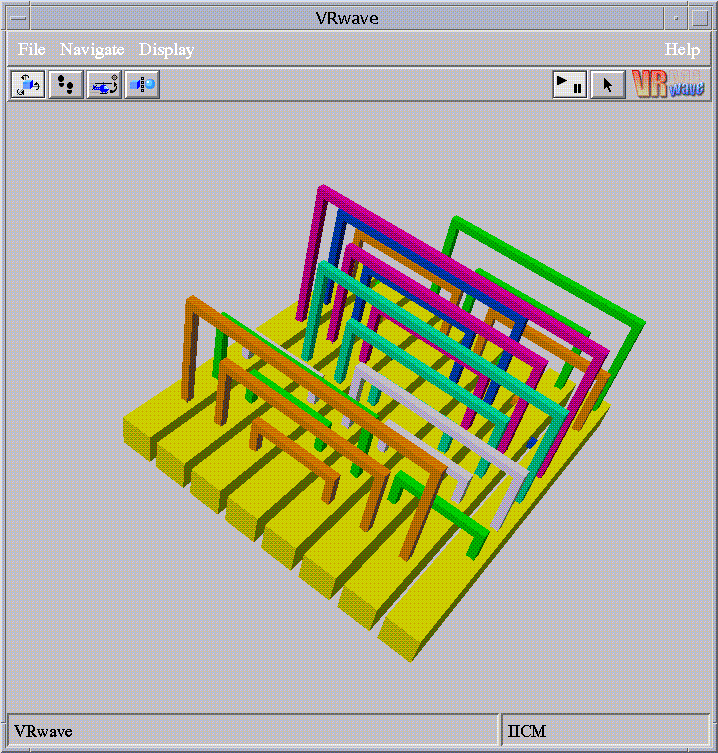
In the same paper simple 1 and 2 bend constructions were given that
require O(n^3) volume. VRML versions of these constructions are
also available:
A typical view of the 2 bend case:

To view the VRML worlds, your browser requires an appropriate plug-in - such as Cosmo Player (for Pcs) or VRWave for Suns. The VRML versions were programmed by S. Gartshore and M. Clossom in June 1998.
If you want to create your own 3-d constructions using these algorithms, try our new software package called ORTHOPAK
This project is funded by NSERC, whose support is gratefully acknowledged.