| Newton's Method (and Intermediate Value Theorem) examples |
| Type | Iteration data | Gif | Animated Gif |
|---|---|---|---|
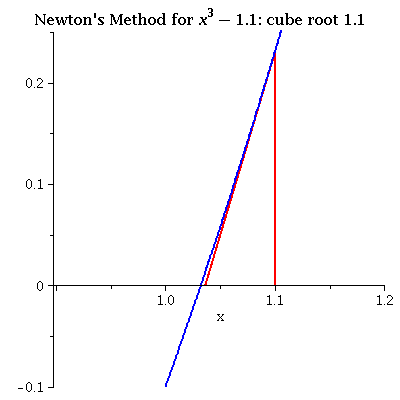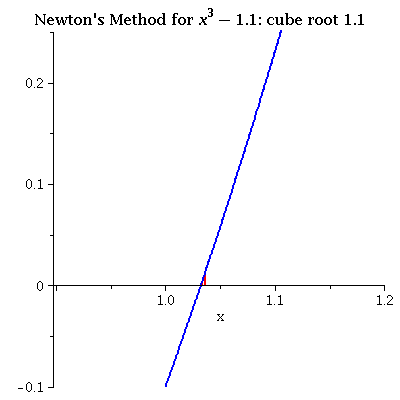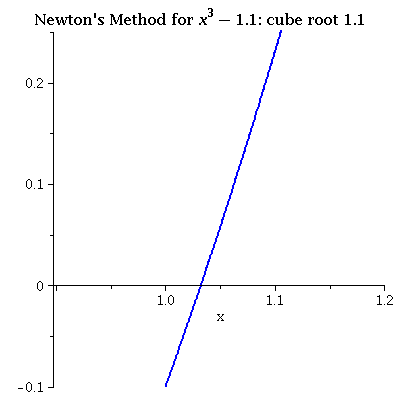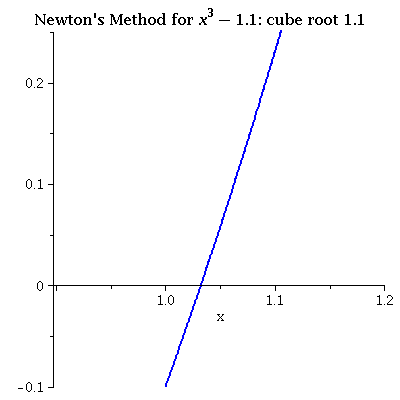
| x3 - 1.1 iterating from 1.1 The initial value is good and convergence is very fast. |
see data | 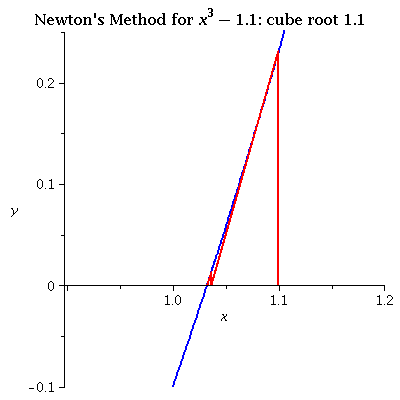 |
 |
| x3 - 1.1 using Intermediate Value Theorem It works but is quite a bit slower than Newton's Method (above) taking 31 iterations to get 8 decimals when starting with [0,2]. |
see data | 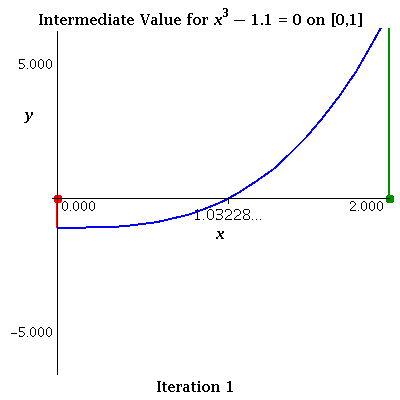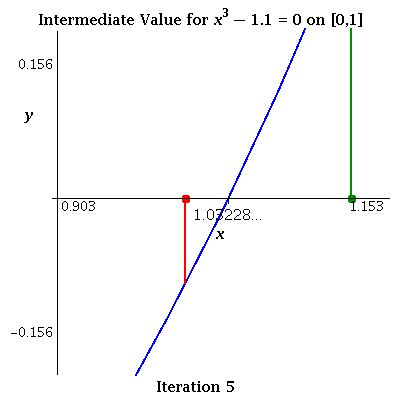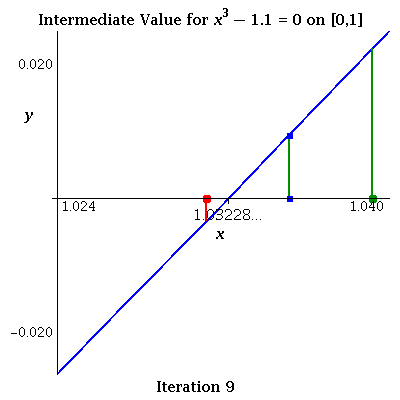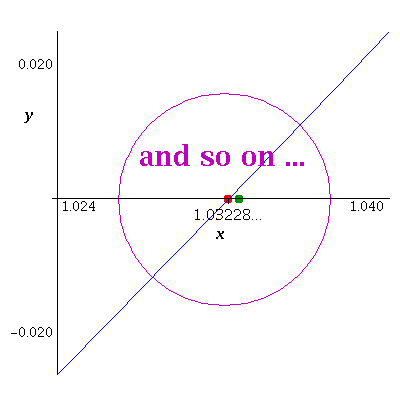 |
|
| x3 - 27 iterating from 27 Even from a relatively distant initial value the convergence can be fast. |
see data | 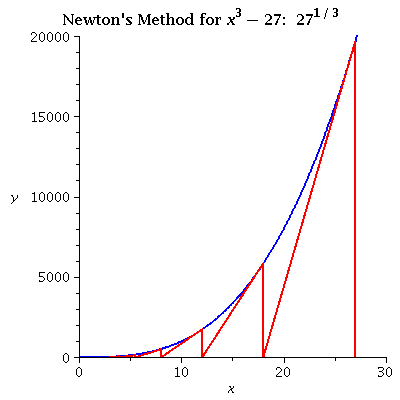 |
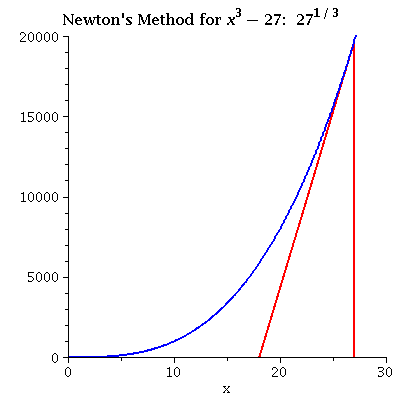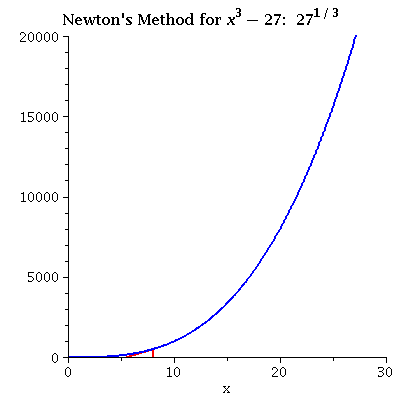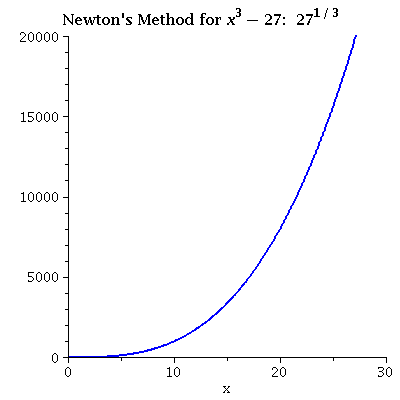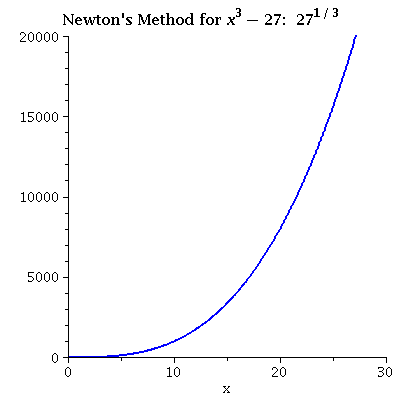 |
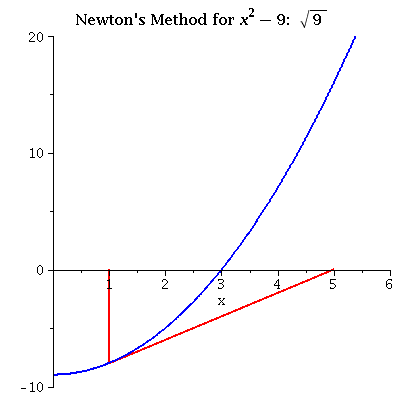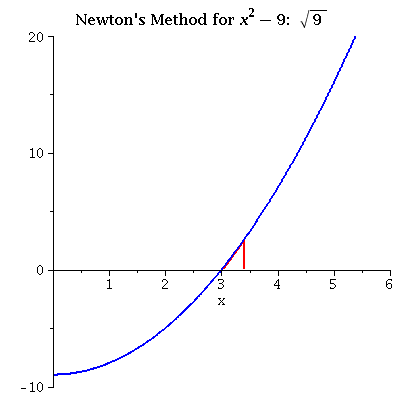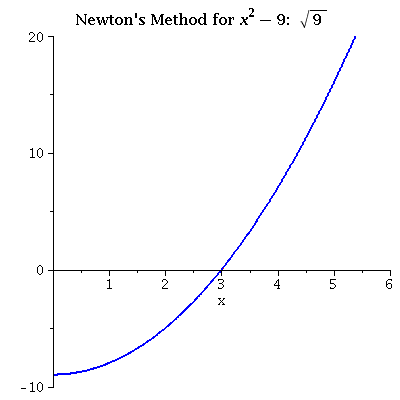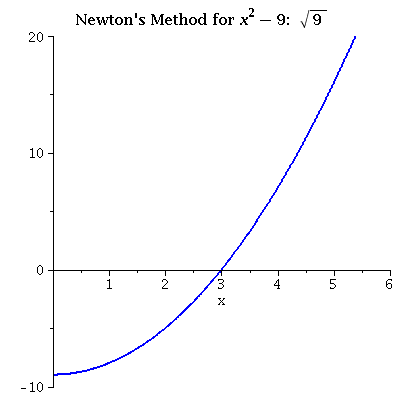
| x2 - 9 iterating from 1 A not particularly good initial value (wrong side) can throw the next interations too far off. |
see data | 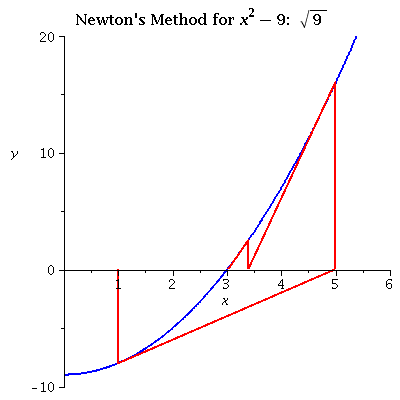 |
 |
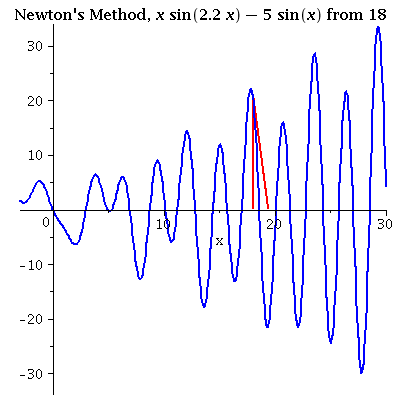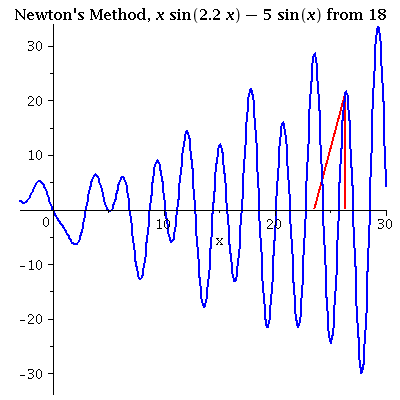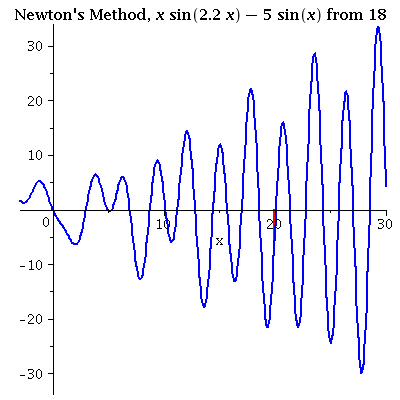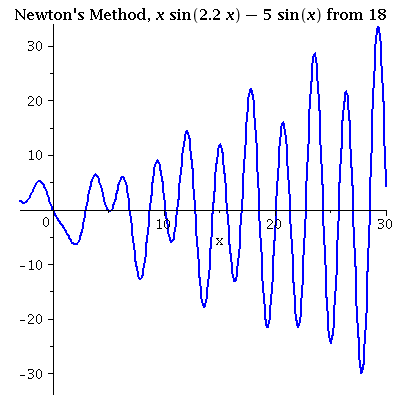
| x sin(2.2 x) = 5sin(x) iterating from 18 A poor initial value may not lead to closest root. Multiple roots are hard to find if the initial value is not close. Interations are near to several different roots in this example. |
see data | 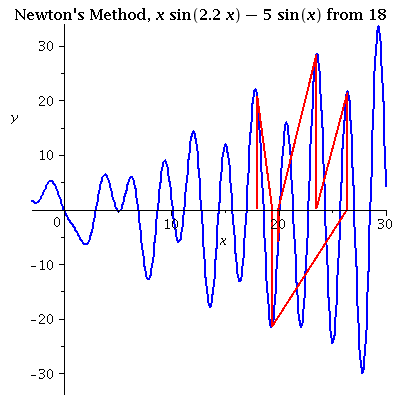 |
 |
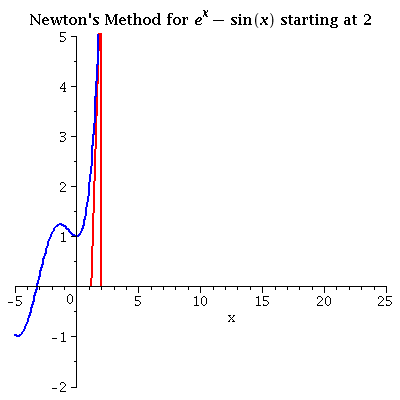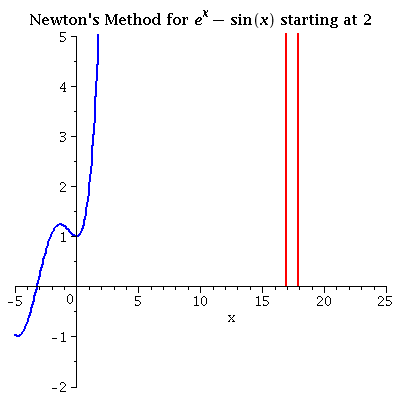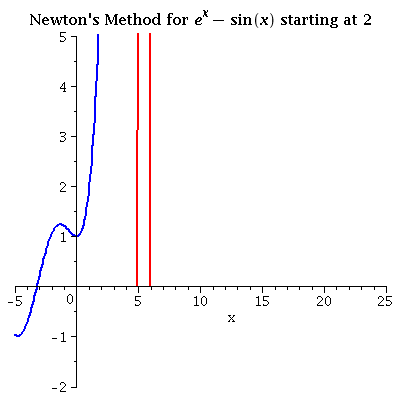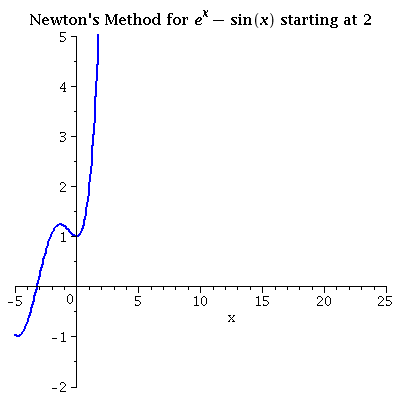
| ex - sin x iterating from 2 Selecting a close initial value is important to avoid "grand tours" like this one! |
see data |  |
 |