
It is generated by a rotation R1 and a reflection r0. Rn denotes the rotation by angle n * 2 pi/6 with respect the center of the hexagon. rn denotes the reflection in the line at angle n * pi/6 with respect to a fixed line passing through the center and one vertex of the hexagon. Take the fixed line to be horizontal in the hexagon:

Then the effects of the elements of the group are as follows:
| id | R1 | R2 | R3 | R4 | R5 |
 |  |  | 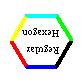 |  |  |
 |  |  | 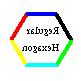 |  |  |
| r0 | r1 | r2 | r3 | r4 | r5 |
The Cayley table is given below. An entry in a row labeled r and column labeled c represents the function composition r(c( )), thus c is applied first to the hexagon. Some people would say that this is backwards and that the conventional notation for function composition is very unfortunate. I'm inclined to agree. The function composition should be (( )r)c and thus the entry on the left, the row, should be the first element applied, in which case the transpose of the following table should be used.
| id | R1 | R2 | R3 | R4 | R5 | r0 | r1 | r2 | r3 | r4 | r5 | |||
| id | id | R1 | R2 | R3 | R4 | R5 | r0 | r1 | r2 | r3 | r4 | r5 | ||
| R1 | R1 | R2 | R3 | R4 | R5 | id | r1 | r2 | r3 | r4 | r5 | r0 | ||
| R2 | R2 | R3 | R4 | R5 | id | R1 | r2 | r3 | r4 | r5 | r0 | r1 | ||
| R3 | R3 | R4 | R5 | id | R1 | R2 | r3 | r4 | r5 | r0 | r1 | r2 | ||
| R4 | R4 | R5 | id | R1 | R2 | R3 | r4 | r5 | r0 | r1 | r2 | r3 | ||
| R5 | R5 | id | R1 | R2 | R3 | R4 | r5 | r0 | r1 | r2 | r3 | r4 | ||
| r0 | r0 | r5 | r4 | r3 | r2 | r1 | id | R5 | R4 | R3 | R2 | R1 | ||
| r1 | r1 | r0 | r5 | r4 | r3 | r2 | R1 | id | R5 | R4 | R3 | R2 | ||
| r2 | r2 | r1 | r0 | r5 | r4 | r3 | R2 | R1 | id | R5 | R4 | R3 | ||
| r3 | r3 | r2 | r1 | r0 | r5 | r4 | R3 | R2 | R1 | id | R5 | R4 | ||
| r4 | r4 | r3 | r2 | r1 | r0 | r5 | R4 | R3 | R2 | R1 | id | R5 | ||
| r5 | r5 | r4 | r3 | r2 | r1 | r0 | R5 | R4 | R3 | R2 | R1 | id |
The orders of the elements are as follows:
| Element: | id | R1 | R2 | R3 | R4 | R5 | r0 | r1 | r2 | r3 | r4 | r5 | |
| Order: | 1 | 6 | 3 | 2 | 3 | 6 | 2 | 2 | 2 | 2 | 2 | 2 |
The subgroups are as follows:
| Elements: | id | R1 | R2 | R3 | R4 | R5 | r0 | r1 | r2 | r3 | r4 | r5 | |
| Subgroups: | |||||||||||||
| Trivial | id | ||||||||||||
| C2 | id | R3 | |||||||||||
| C3 | id | R2 | R4 | ||||||||||
| C6 | id | R1 | R2 | R3 | R4 | R5 | |||||||
| C2 | id | r0 | |||||||||||
| C2 | id | r1 | |||||||||||
| C2 | id | r2 | |||||||||||
| C2 | id | r3 | |||||||||||
| C2 | id | r4 | |||||||||||
| C2 | id | r5 | |||||||||||
| C2+C2 | id | R3 | r0 | r3 | |||||||||
| C2+C2 | id | R3 | r1 | r4 | |||||||||
| C2+C2 | id | R3 | r2 | r5 | |||||||||
| D3 | id | R2 | R4 | r0 | r2 | r4 | |||||||
| D3 | id | R2 | R4 | r1 | r3 | r5 | |||||||
| Full D6 | id | R1 | R2 | R3 | R4 | R5 | r0 | r1 | r2 | r3 | r4 | r5 |